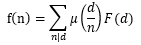Code(BestCoder Round 39)

题目链接：hdu5212

题目大意：给出n个数a[1]..a[n]求出任意两个数的gcd(a[i], a[j]) * (gcd(a[i], a[j]) - 1)之和。

如果我们枚举k = gcd(a[i], a[j])，那么问题就转化为gcd(a[i], a[j]) = k 的个数，这就是我们熟悉的mobius反演了。跟往常一样，构造F(d),f(d):

f(d) = | {(x, y) | gcd(x, y) == d, x <= N, y <= M} |

F(d) = | {(x, y) | (d | gcd(x, y)), x <= N, y <= M} |

并进行反演，可得：

mobius5

由于本题中数的范围不是[1..N]，而是a[i]，因此F(d)需要换一种方法来求得。

我们再来看看F(d)的定义，是所有x，y的公约数(不一定是最大公约数)为d的个数。因此我们仅需要知道a数组中有几个数是d的倍数，设为num[d],则F(d) = num[d] × num[d]

num数组可以O(nlogn)的预处理出来，之后需要枚举最大公约数d求f(d)，这个过程也是O(nlogn)。

在求出f(d)之后，将f(d) × d × (d-1)累加即是要求的结果。

事实上，采用dp的方法也可以O(nlogn)的求出f(d)

根据我们在第一个例题中得出的结论，f(d) = F(d) - f(2d) - f(3d) - ……

则可以从后往前扫一遍求出所有的f(d)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#define N 10240
#define MOD 10007
using namespace std;
int p[N], miu[N], num[N], sum[N], tot, mx;
bool flag[N];
void mobius() {
	memset(flag, 0, sizeof(flag));
	miu[1] = 1;
	tot = 0;
	for (int i = 2; i < N; ++i) {
		if (!flag[i]) {
			p[tot++] = i;
			miu[i] = -1;
		}
		for (int j = 0; j < tot & i * p[j] < N; ++j){
			flag[i*p[j]] = 1;
			if (i % p[j])
				miu[i*p[j]] = -miu[i];
			else {
				miu[i*p[i]] = 0;
				break;
			}
		}
	}
}
int solve1() {
	int ret = 0, tmp;
	for (int i = 1; i <= mx; ++i) {
		tmp = 0;
		for (int j = i; j <= mx; j += i) {
			tmp = (tmp + miu[j/i] * num[j]) % MOD;
		}
		tmp = ((tmp * i) % MOD * (i - 1)) % MOD;
		
		ret = (ret + tmp) % MOD;
	}
	return ret;
}
int solve2() {
	int ret = 0;
	for (int i = mx; i > 0; --i) {
		for (int j = i + i; j <= mx; j += i)
			num[i] = ((num[i] - num[j]) % MOD + MOD) % MOD;
		ret = (((num[i] * i) % MOD * (i - 1)) % MOD + ret) % MOD;
	}
	return ret;
}
int main() {
	int n, ans, tmp;
	mobius();
	while (~scanf("%d", &n)) {
		memset(sum, 0, sizeof(sum));
		memset(num, 0, sizeof(num));
		mx = ans = 0;
		for (int i = 0; i < n; ++i) {
			scanf("%d", &tmp);
			mx = max(mx, tmp);
			sum[tmp]++;
		}
		for (int i = 1; i <= mx; ++i) {
			for (int j = i; j <= mx; j += i)
				num[i] = (num[i] + sum[j]) % MOD;
		}
		for (int i = 1; i <= mx; ++i)
			num[i] = (num[i] * num[i]) % MOD;
		ans = solve1();
		//ans = solve2();
		
		printf("%d\n", ans);
	}
	return 0;
}