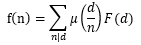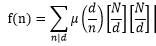Visible Lattice Points(Greater New York 2006)

题目链接: poj3090

题目大意：对于二维坐标系中的点{(x,y)(0 <= x <= N, 0 <= y <= N)}，问这些点中有哪些是原点可以看到的。(原点除外)

题目可以转化为求gcd(x, y) == 1 的有序对(x, y)的数目。

这道题数据范围较小，并且是求x，y互质的数的个数，我们可以采用多种方法来解决。

解法1.欧拉函数

若加一个限制条件：x < y,这其实就是求欧拉函数φ。它的定义是小于等于i的所有与i互质的数的个数。

那么在求出欧拉函数后，乘2就是所有的gcd(x, y) == 1的值了。不过在y = 1时，x和y相等，不用乘2.

另外，这样求的实际上是 1 <= x <= N, 1 <= y <= N的所有情况，还要加上x或y等于0的情况。

欧拉函数可以通过Euler筛法线性得到。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <cstdio>
#include <cstring>
#define N 1024
using namespace std;
int phi[N], p[N], tot;
bool flag[N];
int Euler() {
	int tmp;
    phi[1] = 1;
    tot = 0;
    memset(flag, 0, sizeof(flag));
    for(int i = 2; i < N; ++i) {
        if(!flag[i]) {
            p[tot++] = i;
        	phi[i] = i - 1;
        }
        for(int j = 0; j < tot && i * p[j] < N; ++j) {
            tmp = i * p[j];
            flag[tmp] = true;
            if(i % p[j]) {
            	phi[tmp] = phi[i] * (p[j] - 1);
            }
            else {
            	phi[tmp] = phi[i] * p[j];
            	break;
            }
        }
    }
}
int main() {
	Euler();
	int T, ans, n;
	scanf("%d", &T);
	for (int cas = 1; cas <= T; ++cas) {
		scanf("%d", &n);
		ans = 1;
		for (int i = 1; i <= n; ++i)
			ans += (phi[i] << 1);
		printf("%d %d %d\n", cas, n, ans);
	}
}

解法2.dp

这道题还可以通过dp来解决。其实dp的主要思想和mobius反演相同。我们考虑如下定义的F(d)和f(d):

f(d) = | {(x, y) | gcd(x, y) == d}, x <= N, y <= N} |

F(d) = | {(x, y) | (d | gcd(x, y)), x <= N, y <= N} |

F(d)我们可以很容易求出，它就等于(N / d) × (N / d)，那么如何通过F(d)求出f(d)呢？

我们再来看看F(d)和f(d)的定义，f(d)代表x和y的最大公约数等于d的个数，F(d)表示x和y的公约数(不一定最大)等于d的个数。那么将F(d)中最大公约数大于d的所有个数去掉就是f(d)了。因此我们可以通过枚举d的倍数求出

f(d) = F(d) - f(2d) - f(3d) - ……

根据调和级数的性质，这个可以在O(nlogn)的时间复杂度内完成。我们要求的其实就是f(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <cstdio>
#include <cstring>
#define N 1024
using namespace std;
int num[N], dp[N], n;
int main() {
	int T, ans;
	scanf("%d", &T);
	for (int cas = 1; cas <= T; ++cas) {
		scanf("%d", &n);
		for (int i = 1; i <= n; ++i)
			num[i] = (n / i) * (n / i);
		for (int i = n; i > 0; --i) {
			dp[i] = num[i];
			for (int j = 2 * i; j <= n; j += i)
				dp[i] -= dp[j];
		}
		printf("%d %d %d\n", cas, n, dp[1] + 2);
	}
}

解法3.mobius反演
此外，我们还可以通过mobius反演来求出gcd(x, y) == 1的个数。首先，我们考虑如上含义的f(d)， F(d)，则有

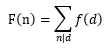
mobius4,

反演得

mobius5

同时还有F(d) = (N / d) × (N / d)，代入反演后的式子则有

mobius5

而我们要求的就是f(1)。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <cstdio>
#include <cstring>
#define N 1024
using namespace std;
int miu[N], p[N], tot;
bool flag[N];
void mobius() {
	memset(flag, 0, sizeof(flag));
	tot = 0;
	miu[1] = 1;
	for (int i = 2; i < N; ++i) {
		if (!flag[i]) {
			p[tot++] = i;
			miu[i] = -1;
		}
		for (int j = 0; j < tot && i * p[j] < N; ++j) {
			flag[i * p[j]] = true;
			if (i % p[j]) {
				miu[i * p[j]] = -miu[i];
			}
			else {
				miu[i * p[j]] = 0;
				break;
			}
		}
	}
}
int main() {
	mobius();
	int T, ans, n;
	scanf("%d", &T);
	for (int cas = 1; cas <= T; ++cas) {
		scanf("%d", &n);
		ans = 2;
		for (int i = 1; i <= n; ++i)
			ans += miu[i] * (n / i) * (n / i);
		printf("%d %d %d\n", cas, n, ans);
	}
}