Visible Lattice Points(Indian ICPC training camp)

题目链接: spoj7001

题目大意：对于三维坐标系中的点{(x, y, z) | 0 <= x <= N, 0 <= y <= N, 0 <= z <= N}，问这些点中有哪些是原点可以看到的。(原点除外)

题目可以转化为求gcd(x, y, z) == 1 的有序对(x, y, z)的数目。

由于是求三个数的最大公约数，此时欧拉函数已经有些局限了，而通过mobius反演仍能简洁的解决该问题。

我们构造f(d), F(d):

f(d) = | {(x, y, x) | gcd(x, y, z) == d, x <= N, y <= N, z <= N} |

F(d) = | {(x, y, z) | (d | gcd(x, y, z)), x <= N, y <= N, z <= N} |

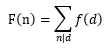
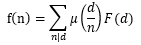
则仍然有mobius4, 反演得mobius5。

此时，F(d) = (N / d) × (N / d) × (N / d)

因此有mobius7

我们要求的仍然是f(1)。

不过此时求出的f(1)是x, y, z 均大于1时的解， 还需加上位于坐标轴和坐标平面上的解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <cstdio>
#include <cstring>
#define N 1000024
using namespace std;
long long miu[N], p[N], tot;
bool flag[N];
void mobius() {
	memset(flag, 0, sizeof(flag));
	tot = 0;
	miu[1] = 1;
	for (long long i = 2; i < N; ++i) {
		if (!flag[i]) {
			p[tot++] = i;
			miu[i] = -1;
		}
		for (long long j = 0; j < tot && i * p[j] < N; ++j) {
			flag[i * p[j]] = true;
			if (i % p[j]) {
				miu[i * p[j]] = -miu[i];
			}
			else {
				miu[i * p[j]] = 0;
				break;
			}
		}
	}
}
int main() {
	mobius();
	long long T, ans, n;
	scanf("%lld", &T);
	while(T--) {
		scanf("%lld", &n);
		ans = 3;
		for (long long i = 1; i <= n; ++i)
			ans += miu[i] * (n / i) * (n / i) * ((n / i) + 3);
		printf("%lld\n",ans);
	}
}