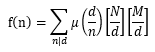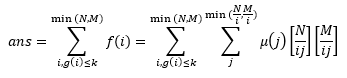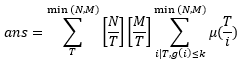Mophues(Asia Regional Hangzhou Online 2013)

题目链接hdu4746

题目大意：有Q个询问，对每个询问，给出N，M，P，求 1 <= x <= N，1 <= y <= M 中满足 gcd(x, y) 的质因子个数 <= P 的有序对(x, y)的对数。(如12 = 2 × 2 × 3，则其质因子个数为3)

本题和以前不同的是，我们要求的并不是gcd(x, y)等于某个定值了，而是需要gcd(x, y)满足一定的条件。无论如何，根据以往的经验，我们先定义F(d)和f(d)：

f(d) = | {(x, y) | gcd(x, y) == d, x <= N, y <= M} |

F(d) = | {(x, y) | (d | gcd(x, y)), x <= N, y <= M} |

并进行反演，最后可得：

mobius8

设g(x)表示x的质因子的个数，则我们要求的事实上是：

mobius10

但是直接这样算肯定是要超时的，我们设T = i × j，则原式可化简为：

mobius11

我们如果预处理出对每个T的μ函数之和，即可在线性时间复杂度内求出结果。

不过，本题还有多个询问，因此需要对求出的μ函数之和再求前缀和，从而通过上一道例题中提到的分段的方法快速求解。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <cstdio>
#include <algorithm>
#define N 500010
using namespace std;
typedef long long ll;
int miu[N], p[N], tot, flag[N];
ll ans, sum[N][32];
void mobius() {
	miu[1] = 1;
	tot = 0;
	flag[1] = 0;
	for (int i = 2; i < N; ++i) {
		if (!flag[i]) {
			p[tot++] = i;
			miu[i] = -1;
			flag[i] = 1;
		}
		for (int j = 0; j < tot && i * p[j] < N; ++j) {
			flag[i * p[j]] = flag[i] + 1;
			if (i % p[j]) {
				miu[i * p[j]] = -miu[i];
			}
			else {
				miu[i * p[j]] = 0;
				break;
			}
		}
	}
	for (int i = 1; i < N; ++i)
		for (int j = i; j < N; j += i) {
			sum[j][flag[i]] += miu[j / i];
		}
	for (int i = 1; i < N; ++i)
		for (int j = 0; j < 20; ++j) {
			sum[i][j] += sum[i - 1][j];
			if (j)
				sum[i][j] += sum[i][j - 1] - sum[i - 1][j - 1];
		}
}
int main() {
	mobius();
	int T, a, b, k;
	scanf("%d", &T);
	while (T--) {
		scanf("%d%d%d", &a, &b, &k);
		int lim = min(a, b), nxt;
		ans = 0;
		k = min(k, 19);
		for (int i = 1; i <= lim; i = nxt + 1) {
			nxt = min(b / (b / i), a / (a / i));
			ans += (ll) (sum[nxt][k] - sum[i - 1][k]) * (b / i) * (a / i);
		}
		printf("%I64d\n",  ans);
	}
	return 0;
}