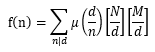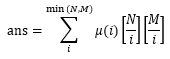GCD(Sunline Cup 2008)

题目链接hdu1695

题目大意：有Q个询问，对每个询问，给出N，M，k，求 1 <= x <= N，1 <= y <= M 中满足 gcd(x, y) = k 的无序对(x, y)的对数。

若先不考虑无序，根据我们前面的经验，构造f(d), F(d):

f(d) = | {(x, y) | gcd(x, y) == d, x <= N, y <= M} |

F(d) = | {(x, y) | (d | gcd(x, y)), x <= N, y <= M} |

则可知F(d) = N / d × M / d。通过mobius反演可得到：

mobius8

则我们要求的是f(k)。事实上，若gcd(x, y) = k，则 gcd(x / k, y / k) = 1。将N、M分别替换为N / k、 M / k，问题就转化为我们熟悉的求f(1)的问题了。即：

mobius9

此外，我们观察函数g(i) = N / i，它的函数值是一个分段函数，且每一段均为常数。因此我们如果预处理出μ函数的前缀和，则对每一段都可O(1)的求出结果。总的复杂度为O(sqrt(n))

这样求出来的是有序对(x, y)的数量，还需要去重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <cstdio>
#include <algorithm>
#define N 100010
using namespace std;
typedef long long ll;
int miu[N], p[N], tot, sum[N];
bool flag[N];
ll ans, ans2;
void mobius() {
	miu[1] = 1;
	tot = 0;
	for (int i = 2; i < N; ++i) {
		if (!flag[i]) {
			p[tot++] = i;
			miu[i] = -1;
		}
		for (int j = 0; j < tot && i * p[j] < N; ++j) {
			flag[i * p[j]] = true;
			if (i % p[j]) {
				miu[i * p[j]] = -miu[i];
			}
			else {
				miu[i * p[j]] = 0;
				break;
			}
		}
	}
	sum[0] = 0;
	for (int i = 1; i < N; ++i)
		sum[i] = sum[i - 1] + miu[i];
}
int main() {
	mobius();
	int T, a, b, c, d, k;
	scanf("%d", &T);
	for (int cas = 1; cas <= T; ++cas) {
		scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
		if (k == 0) {
			printf("Case %d: 0\n", cas);
			continue;
		}
		b /= k;
		d /= k;
		int lim = min(b, d), nxt;
		ans = ans2 = 0;
		for (int i = 1; i <= lim; i = nxt + 1) {
			nxt = min(b / (b / i), d / (d / i));
			ans += (ll) (sum[nxt] - sum[i - 1]) * (b / i) * (d / i);
		}
		for (int i = 1; i <= lim; i = nxt + 1) {
			nxt = min(b / (b / i), d / (d / i));
			ans2 += (ll) (sum[nxt] - sum[i - 1]) * (lim / i) * (lim / i);
		}
		ans -= ans2 / 2;
		printf("Case %d: %I64d\n", cas, ans);
	}
	return 0;
}