1月25日到2月1日,在北京举行了ICPC Camp 2016。我校4支队伍参加了这次Camp。
Day1. 1.25
Day2. 1.26
Day3. 1.27
Day4. 1.28
上午,Google Code Jam Final选讲。由培根爷向我们讲解了一些Google Code Jam中的趣题。
下午,举行了第四次训练赛,Grand Prix of China。
A. Graph Drawing
知识点
费用流 + 建图技巧
题目大意
给出n~200个点,然后给出m < n - 2个逆时针的图形,要求n个点的分布满足:这些个图形的边都是水平的和垂直的. 如果不是水平和垂直的,需要加一个点,然后变成水平和垂直的.每加一个点就多用一个代价.问加点个数最少的加点的个数.
做法
带下界的费用流,点向图形流4个,因为每个都是90度,然后图形与图形之间有一个公共边,那么就连一个费用为一的,流为INF的流,然后图形向终点连2n-4个流,注意有一个大的矩形,它的点的度数就是它里面的点的个数2 + 4. 是这样建图,根据360分成90度.但是不知道细节了…
B. Dominating Set
知识点
状压dp
题目大意
给出一个n个点,m条边的二分图($1 \leq n \leq 30,0 \leq m \leq 255$)。现在要选择一个该图的点的子集,使得对于图中的任何一个点$v_i$,要么它本身存在于该子集中,要么存在一个和它相邻的点在该子集中。求这样的子集的个数。
做法
首先我们二进制枚举小的那一边,$2^{15}$,表示强制只使用这么多.然后它向右边一些点连边(设为A类点),那些点之外(B类点)的就一定要选,之后左边还剩一些不能选的,只能通过右边A类点再选一下才能覆盖,那么这个的情况数就很多了.我们现在解决的是左边要覆盖到mask(注意可以多)的点,右边的点有多少种选择.我们现在先算恰好覆盖mask的左边的点,发现这是可以预处理的,因为右边确定选的点一定和这些点没关系,接着我们mask枚举最后一个选的点,然后利用恰的性质,$2^{num} - 1$, 为系数转移. 然后弄出来恰之后,高维前缀和求和,题目就解决了
C. Balls and Bins
知识点
二分图匹配 + 动态修改权值
做法
还未弄懂
D. Attack
知识点
随机化? | 树链剖分 + dfs序 + 线段树维护
做法
还未弄懂
E. Graph Automorphism
一道非常难的题,在听完讲解后明白了大体的解题思路,因为原图中度大于$3$的点最多只有$10$个,所以可以对这些点进行爆搜。就先当作一个思路记录下来吧。
F. Similar Subsequence
知识点
dp
题目大意
给出一个序列$A$和序列$B$,问序列$B$中是否存在一个子序列和$A$序列相似。
相似的定义为
对于${a[1] \dots a[n]}$和${b[1] \dots b[n]}$,$a$和$b$相似当且仅当对所有$1 \leq i,j \leq n$,满足$(a[i]-a[j])(b[i]-b[j]) > 0$
此外,$A$序列存在一个特殊性质,即$A$中的任意一个三个元素的子序列都不会和序列${2,1,3}$或序列${2,3,1}$相似。
做法
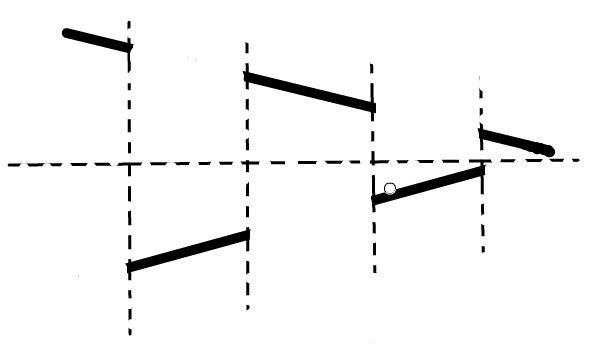
首先,我们可以发现,由于$A$序列的特殊性质,$A$序列的形状如下图所示:
因此,我们从前往后枚举时,相当于后面的点都要大于前面的最小值,小于前面的最大值,因此一个显然的dp状态是$f[i][j][min][max]$,表示从数列$B$的前$i$项中取$j$项,当前项对应于$A$数列的$A_j$,当前数列的最小值为$min$,最大值为$max$,此状态是否能达到。但是这是一个$O(n^4)$的dp,时间复杂度难以承受。
所以我们就想到将$min$或$max$其中一维变为dp的值,也就是$f[i][j][min]$为当前状态的最大的$max$,这样dp记录的信息没有减少,但时间复杂度变为了$O(n^3)$。
赛场上我们想偏了,由于发现$A$序列可以分为上下两部分,所以我们想了一个枚举分界线,之后在两边分别dp算最长上升及最长下降子序列,之后再dp合并的方法。但是发现这种方法做不了。这还是因为没有发现$A$序列更优美的性质。
G. Random Arithmetic
知识点
dp + 数学
题目大意
给出$n$个数$a[1] \dots a[n]$,每次从中随机选择两个数$a[i], a[j]$,将其随机进行$a[i] + a[j]$或$a[i]*a[j]$的操作,并将操作后的数放回原序列中,这样进行$n - 1$次后,最终会得到一个数。我们要求这个数的期望。
做法
首先,最终结果一定是一个多项式,我们利用分配律把多项式中的括号全部打开,变成一个$X$项的多项式,多项式中每项为$\prod\limits_{a[j] \in S} a[j]$,其中$S$为此项中所含的原数列中的树的集合。
由于数组$a$中的每个元素的地位是等价的,因此对于$|S|$相同的项,其出现的概率是相同的,设为$p$,则我们要求的答案其实为
$$\sum\limits_{j = 1}^n p[j]$$
$$\sum\limits_{|S| = j} $$
$$\prod\limits_{a[i] \in S} a[i]$$
对于集合个数为j的所有子集的乘积,很容易通过$O(n^2)$的dp求出,现在要求的就是每一个集合个数对应的系数,也就是在所有情况中的出现次数。
由于所有的$a[i]$地位等同,因此我们要求的相当于在原数组中选出前$j$个元素组成一项时这一项的出现次数。我们定义状态$p[i][j]$表示考虑到前$i$位,组成的项中的元素个数为j时的出现次数,那么只需要枚举当前数是和哪个数结合,就可以写出转移方程。
H. Optimal BST
知识点
dp优化——决策单调性
题目大意
给出一个$n$($n \leq 4000$)个节点的树,每个节点上有一个数$a_i$。对每个节点,从根节点到它都有一条路径序列,求每个序列的$OPT$。
$OPT$的定义为:$OPT[i][j] = min(OPT[i][k] + OPT[k + 1][j] + \sum\limits_{t = i}^ja[t])$
做法
首先,我们可以有一个最直接的dp方法,裸的dp是$O(n^3)$,但是可以发现这个dp可以使用四边形不等式优化,从而使复杂度降到$O(n^2)$。
但是这种方法是错的。因为本题要在树上dp,对于一个分叉节点,如果采用从上到下的枚举方式dp的话,在从一棵子树中的链转移到另一棵子树中的链时,四边形不等式中已确定的转移状态会回滚,重新计算。这样在最坏情况下会退化到$O(n^3)$。
我们换一种方式进行dp,即从下到上枚举起始位置,对每一个起始位置,再采用$f[i][j] = \min \limits_{ 1 \leq k < j} (f[i][k] + f[k + 1][j] + S)$的方程进行转移。这时我们相当于固定第一维$i$,方程变为了$f[j] = min(f[k] + w[k][j])$的形式,此时由于$w$数组为单调的,可以使用决策单调性进行优化。
即使用一个栈记录有用的转移位置,每次在栈中二分查找当前的转移位置,转移之后再用当前状态更新栈。这样的时间复杂度为$O(n^2 \log n)$
I. Boxes on tree
知识点
最小树形图
题目大意
给出一个n个节点的树,树上的每个节点都有一个编号$i$,此外树上的每个节点还放置了一个编号为$p[i]$物品。我们要做的是通过一个机器人使树上的所有物品都放回到它所对应的编号的位置。机器人最开始在1号节点,且机器人每次只能携带一个物品进行移动。机器人每到一个节点,都可以将当前携带的物品暂时放在这个节点,之后再取出这个节点上原本放置的物品,继续进行移动。此外,机器人在将所有的物品放回原位后需要再返回1号节点。问机器人的最小步数。
做法
根据题意可知,物品相当于一个编号的排列$P$,根据排列的性质,我们可以知道,这些物品一定可以构成若干个环。物品只会在环内移动。因此,我们可以先将所有的环求出来。
每一个环包括这个环中所有的原排列中的$P_i$,以及从原排列中的一个元素到下一个元素的过程中所经过的点。我们记在原排列中的点为关键点,从原排列中一个元素到下一个元素中经过的点位非关键点。那么我们可以以如下的方式建一个有向图。
将每一个环看作有向图中的一个顶点。忽略点的个数为1的环(这样的环不需要机器人进行处理,自己就已经满足条件了,不过如果1号节点是一个这样的环的话还是要加入有向图中,因为机器人要从这个点开始跑)
在有向图的任意两个节点之间创建有向边$(u,v)$,边权为$u$点所代表的环中的任意一点到$v$点所代表的环中的关键点的最短距离。
之后我们从1点所在的环出发,跑一遍最小树形图,最终答案就是 所有环的长度和 + 最小树形图中的所有边 × 2
之所以以上述方式建图,是因为机器人可以在任意点放下当前装载的物品,并拾起该点上的物品,之后将该物品放置其所在的位置,再重新返回此点,拾起之前放下的物品。之所以建有向图,是因为机器人可以从一个环中的非关键顶点走到另一个环中的关键点。因此要用有向图来描述。
答案的计算很容易就可以想清楚。
J. Welcome to ICPCCamp 2016
知识点
乱搞 | 结论 + 构造
题目大意
给出$6666$个在$1$~$2016$之间的数,让你从中挑恰好$2016$个数,使得$这些数的和 \equiv 0 \ \ mod \ \ 2016$。
做法
sol.1
赛场上我们采用了一种比较奇怪的方法通过了这道题。
首先很容易可以想到一种 $O(6666 \times 2016 \times 2016)$ 的dp。
就是 $f[i][j][k]$ 表示从前 $i$ 个数中取 $j$ 个,模为 $k$ 的状态是否合法。但是这样显然无法通过这道题。
由于每个数的大小都在$1$到$2016$之间,因此我们可以先统计出每个数字出现的次数,之后每次从较大的一堆中取出一个数,这样取出大约$1966$个数,剩下大约$4000$个数。我们接下来要做的就是从$4000$个数种选出$50$个数。但是这样$n$还是有些大,我们就从这$4000$个数中尽量均匀的取出$100$个,在大多数情况下都可以找到满足条件的解。
sol.2
赛场上还有其他通过随机做法解决这道题的。大致思想就是每次随机打乱原序列,那么我们可以认为一定存在一种序列,其中存在连续的$2016$个数满足题目中的条件。这可以$O(n)$的做出来。
sol.3
上面介绍了两种乱搞解法,下面介绍一下标程的做法。
首先,有如下定理
对于任意$2n-1$个数,总能从中选出$n$个数$a[1] \dots a[n]$,使得$ \sum\limits_1^n a[i]\ \ \equiv 0 \ \ mod \ \ n$
根据这个定理,我们可以构造出在$n = pq$时的一种解决办法。
首先,从$2p-1$个数中可以选出$p$个数使得其相加模$p$等于$0$
我们进行$2q - 1$次这样的操作,那么就相当于得到了$2q-1$个$p$的倍数(注意此时还剩了$p-1$个没有凑成p的倍数的数)。
再从$2q-1$个数中挑出$q - 1$个数,那么它们的和相加一定是q的倍数
这样,我们就挑出了$pq$个数,其和是$pq$的倍数。我们需要原数列中元素的个数为$(2q-1)p + p - 1$即$2pq-1$个数。
我们看一下$2016$的质因子,$2016 = 2^3 \times 3^2 \times 7$,我们把它拆分成两个较小的数,这样就可以通过最开始的三维dp来解决子问题,之后再使用一次三维dp解出原题中的问题。
这种方法只要求有4031个数就一定可以找出一组解了,题目中给了6666个数就是为了让一些队伍使用乱搞的解法来解决这道题。
Day5. 1.29
今天没有比赛和培训。Camp请了几个上交的学长来给我们做了一些以后的方向选择、人生规划方面的讲座,并举行了Camp大赛(Osu!、炉石、斗地主)。