这次选拔赛都是一些考思想的题目,没有模板题,只不过有些题目描述过于晦涩,较难理解。最近感觉做这种类型的题目偏多,是时候刷一些模板题了……
A.Martix
很简单的dp。
题目大意:给出一个矩阵A,求出矩阵B, 满足
B[i,j]=min{ A[x,y] : (y>=j) and (x>=i+j-y) }
预处理出F[i][j]为位于(i,j)位置右下方的数的最小值,则很容易写出状态转移方程:
B[i][j] = min(B[i-1][j+1], F[i][j])
B.Tower of Hanoi
也是很简单的递推。
题目大意:对于Tower of Hanoi游戏,给出将一个盘子从一根柱子转移到另一根柱子的花费,求将n个盘子从第一根柱子转移到第三根柱子的最小花费。
为了叙述方便,将三根柱子命名为a,b,c。将i个盘子从柱子t转移到柱子k有两种方法:
方法1:
- i-1个盘子从a转移到b;
- 第i个盘子从a转移到c;
- i-1个盘子从b转移到c。
方法2:
- i-1个盘子从a转移到c;
- 第i个盘子从a转移到b;
- i-1个盘子从c转移到a;
- 第i个盘子从b转移到c;
- i-1个盘子从a转移到c。
从这两种情况中取最优即可。
C.Martix
构造。
题目大意:对一个 2^n 行, 2^m 列的矩阵,将 0 ~ 2^(n+m) -1 填进去,使得矩阵中相邻的数的二进制均相差1,最左边和最右边,最上边和最下边也是相邻的。
这其实是一个格雷码的扩展问题。可以采用和格雷码相似的构造方法,分形倍增或直接采用异或构造均可,这里介绍分形倍增的构造方法。
首先将0和1分别填入矩阵的(0,0),(0,1)位置,之后对横竖两个方向进行倍增,每次将已有的数倒序复制过来,然后在二进制的最前面加一个1(相当于每个数加了 2^i ),这样即可保证题目要求。
D.Join the Strings
贪心。
题目大意:将给出的n个字符串串联起来,使得所得的字符串字典序最小。
注意直接按照字典序排序是不对的,一种较为简单的方法是重载string的<运算符,对于两个字符串a、b的比较,如果字符串ab的字典序小于字符串ba的字典序,则返回a < b。这样可以正确的给字符串排序。
E.Idempotent Filter
题目描述不太清楚,如果读懂题了就很容易解出。
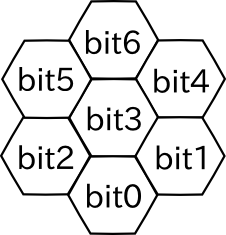
题目大意:给出一个128位的01串c,这个串表示一种变换规则,它的含义是图中位置为3的格子会变为c[i]。其中i = sum( bit[j] × 2^j )。bit[j] 是指位置为j的格子的数字。
如果我们应用了两次这种规则和应用一次这种规则效果相同(即应用了一次规则后再次应用这种规则原图不会发生任何变化),就称这种规则为幂等的。 对于给出的规则,请你判断他它是不是幂等的。
我们可以知道某个格子的变化只与和他相邻的格子有关。由于需要判断应用两次规则与应用一次规则效果是否相同,因此仅对他应用规则是不够的,还需要对和他相邻的格子相邻的格子应用规则,应用一次规则后,他和他相邻的6个格子均有可能发生变化,之后在对他应用这个规则,检查他有没有再次变化即可。 需要枚举的时间复杂度为 2^19 ,可以接受。
F.Flowers
三分或贪心
题目大意:给出n种花,每种花有一个临界值,如果它的营养超出了临界值就会开,所有花的初始营养值均为0.给花浇水或施肥会导致他们的营养值发生变化。浇水和施肥都有花费,求使所有花开的最小花费。
比赛时虽然也想到了三分,但是由于没有仔细证明正确性,最后还是选择了贪心的写法,不过三分思维量更加小。
贪心的话,就是判断当前是浇水好还是施肥好。因为如果浇的水确定了的话,那么让所有花开的花费就已经确定了。通过先求出让所有的花全都施肥的单位花费,可以o(1)的判断当前是浇水好还是施肥好。总的时间复杂度是O(nlogn)。
G.Square in Circles
二分+线段覆盖
题目大意:给出n个圆,每个圆圆心都在x轴上且每没有相互包含的圆。求在这些圆覆盖的面积中存在的最大的正方形的变长。
最开始我以为正方形的边长只有可能是圆半径的根号2倍或是两个圆相交的割线长,后来才发现以割线为边长有可能不能构成一个正方形,于是就想到了二分。
但是仅仅是局限于两个圆里的二分,仍然不能处理所有情况。
后来在tangjz同学的指点下,才想明白了二分边长之后直接把每个圆在保证当前边长的前提下的最宽的宽度以线段的形式记录下来,那么只需要判断这些线段合并之后有没有一条长度大于等于二分的边长即可。
H.Coockie Counter
dp
题目大意:有n个糖果需要d天吃完,每天可以不吃,但最多吃x-1颗,问有多少种吃法。
由于天数非常大,有许多天都是一颗糖都不吃的,我们可以先忽略这种情况,假设每天都至少吃一块糖。设f[i][j]表示i天吃了j块糖的情况数,那么最终结果就是在d天中选i天吃糖,
ans = sum(f[i][n] × C(d,i))
但是朴素的dp状态转移是O(n)的,会超时,于是我们可以再用一个数组记录f[i][j]的前缀和,这样就可以O(1)的进行状态转移。总的时间复杂度是O( n^2 )。
I.The King’s Ups and Downs
题目大意:给出n个不同的数,求把它们排列成一个交错的数列有多少种排法。
之前做过类似的题目。题目要求的序列有两种情况:
- 大小大小大……
- 小大小大小……
设长度为i的第一种序列的个数为f[i],第二种序列的个数为g[i]
则通过枚举最大的数的位置,可求出他们之间的转换关系:f[i] = sum(g[j-1] × g[i-j] × C(i,j-1))
并且可发现f[i] = g[i] 因此f和g仅求一个即可。
J.Students’ Revenge
贪心
题目大意:同学们从n个工作中选出p个让学生会去做,学生会只能从这p个工作里面选k个去做,每个工作如果被做了会增加学生会的劳累值,如果不被做会使校领导不高兴。学生会首先会保证校领导不高兴的值尽量小,然后会使他们的劳累值尽量小,而学生们首先想要学生会的劳累值尽量大,然后会让校领导尽量不高兴。问学生该如何选择这p个工作。
读题就读吐了……
首先选出p-k个不高兴值最小的,这些工作学生会肯定不会去做。
之后从剩下的里面选出k个劳累值尽量大的,这样就保证了学生会的劳累值最大,
之后从剩下的n-p个加上之前的p-k个里面选p-k个不开心值尽量大但是小于之前选定的k个里面最小的不开心值的工作。 这样就保证了校领导的不开心值最大。
注意如果出现相等的情况一定要考虑清楚。