第十届北航程序设计竞赛网络赛题解

发表于

这次网络赛题目都不算太难，3天的时间在和HJK童鞋讨论后共做出了11题，一些题目也是讨论了很久才想通的，感觉是一场质量不错的比赛。

###A.C.D.F.L.M

水题，也不贴代码了，只要仔细想一下就很容易想出解法的。

###B.AC自动机+状态压缩

题目大意是求n的倍数中{包含给出的k个（k<=5）数字}的最小的数

我们先根据给出的k个数字建立AC自动机，设状态f[i][j][mask]为当前的数字modn为i，并且当前在自动机的j号节点上，当前数字中已经出现过mask这个集合中的串了。 则初态为f[0][0][0]，终态是f[0][x][全集]。

所以我们需要找一条从初态到终态的路径，使得走过的路径构成的数字串尽可能小。数字最小首先要位数最小，然后字典序最小。所以只需要从初态开始宽度优先搜索，按字典序的顺序扩展状态，第一个访问到的终态的路径就是答案。

在AC自动机中每走一步，都需要看当前的后缀是否为某几个数字（通过last数组），f数组需保存走到这个状态的最后一个节点，以及这个节点是从那个节点转移过来的（三个下标），找到答案后递归输出结果。

注意数字串是不能有前导0的，最后答案里也不会出现-1。 时间复杂度为O(nmlogX2^m)

###E.dp+容斥

题目大意是算两个概率：

  1. n个点每个点的值都不小于f1
  2. n个点中有不少于连续k个点的值不小于f2 （每个点可取值的范围为1~p）要求的结果是p=p(1)∪p(2)

根据容斥原理 p=p(1)+p(2)-p(12) 而 p(12) = p1 × p(2|1)

第一种情况的概率很容易求得

第二种情况可通过dp求得：

  • 设计状态f[i]表示仅考虑前i个数，满足所求限制的概率。
  • 第i个数有两种选择：小于f2或大于等于f2
  • 若第i个数小于f2，则f[i] = f[i-1]
  • 若第i个数大于等于f2，则f[i] = f[i-1] + f[i-k-1] × p(连续k-1个数大于等于f2) × p(第k个数小于f2)

最后的表达式：

1
2
3
4
5
6
7
8
if (i < k)
	f[i] = f[i-1];
else if (i == k){
	f[i] = pow(tp, k);
}
else {
	f[i] = f[i-1] + pow(tp, k)*(1-tp)*(1-f[i-k-1]);
}

tp表示大于等于f2的概率。求p（2|1）只需要修改tp的值即可

另外，由于2*k>n因此最多只有一段满足连续k个点的值不小于f2，可以直接算出概率

###G.dp | 悬线法

题目大意给出一个矩形，矩形中每个点都为W或B求所有的矩形满足举行中既有W又有B

我们可以通过dp找出所有的只含W或B的矩形。

f[i][j]表示以点(i,j)为右下角的仅含某种矩形的个数

仅考虑只含W的矩形。首先预处理出每个(i,j)当前列的W字符的高度。

对f[i][j]而言，若h[i][j]>=h[i][j-1]那么对以(i-1,j)为右下角的每一个矩形，都一一对应一个以(I,j)为右下角的矩形，f[i][j] = f[i-1][j]

若h[i][j]<h[i][j-1]，那么我们找出在第j列前第一个高度小于h[i][j]的列t，那么在这两节列之间的矩形可取宽度最宽为j-t，高度最高为h[i][j]的所有矩形，另外，对每一个f[i][t]都唯一对应一个f[i][j]因此

f[i][j] = f[i][sta[top]] + (j-sta[top])*h[i][j]

Sta[top]为单调栈，用来存储第一个小于h[i][j]的列标号。

仅含B的矩形用类似方法也可得出

最终结果为Ans=sum-sum（W）-sum（B）

###H.建图优化+MST

题目大意：给出平面上n个点，求最小生成树。这n个点分布在三条平行于y轴的直线上。

显然对于同一条垂直于横坐标轴的直线上的点，只有相邻两个点间的边需要建。 对于不在同一条垂直于横坐标轴的直线上的两个点，考虑Kruskal算法的实现过程。

pic

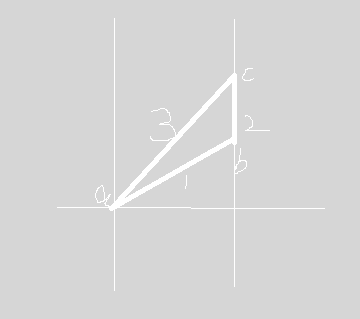
1、2号边都比3号边要短，所以在枚举到3号边的时候，a、b两点必然已连通，b、c两点必然已连通。所以a、c两点也连通了。所以3号边有没有都无所谓。

因此每个点只需与纵坐标比不比自己小的最小的一个点还有纵坐标不比自己大的最大的一个点连边，连出的图类似锯齿形。边的数量为O(n)级别,求最小生成树即可。

###I.数位dp

题目大意：
设函数f(x)为一个数各个位上数字之积。现给出L,R,X，求[L,R]之间有多少符合的i使得f(i)=x;
我们设dp[i][sta][limit][zero]表示枚举到第i个位置，当前位置的乘积为sta的符合条件的个数。（limit和zero用来记录当前是否有前置0，是否为限制位）

则我们要求的结果是dp[len-1][x][1][0]+dp[len-2][x][0][1]

但是状态太多，我们只保存在limit为0且zero为0时的dp[i][sta]这样，每次计算不需要清空dp数组。

转移方程：

zero为0时:

1
2
3
4
5
6
7
8
9
10
11
int last = lim ? dig[pos] : 9;
for (int i = 1; i <= last; ++i) {
	if (sta % i == 0) {
		if (i == dig[pos] && lim) {
			ans += dp(pos-1, sta/i, 1, 0);
		}
		else {
			ans += dp(pos-1, sta/i, 0, 0);
		}
	}
}

zero为1时：

1
2
3
4
5
6
ans += dp(pos-1, sta, 0, 1);
for (int i = 1; i <= 9; ++i) {
	if (sta % i == 0) {
		ans += dp(pos-1, sta/i, 0, 0);
	}
}

数位dp每次只保存没有限制的状态，这样dp数组可以重复利用。

###J.数学公式

题目大意：求把n的全排列的每一种情况通过交换两个数的位置变为1..n所需要的交换次数的期望

如果每个pi向他应该在的位置连一条边，注意到每个点有且仅有两条边（可能是自环），那么最终的图一定是k个互相没有交集的环。而且每条长度为i的环需要的交换次数为i-1，因此这题转换为求长度为i的环出现的概率。

我们从n个点中选取i个，那么除这i个之外的点随便排，这i个点由于要成环，那么我们固定一个点，剩余的点可以随便排。

公式为p(i) = C(n,i) × (n-i)! × (i-1)! / n!

另外，设f[i]表示i的全排列变为1..n所需的交换次数的期望，我们可以写出一个简单的递推式:f[i] = 1/n × f[i-1] + (n-1)/n × (f[i-1]+1)

这个递推式两边同乘i!，可得出g[i] = i × g[i-1] + (i-1) × (i-1)!

其中 g[i] = i! × f[i]

我们要求的就是g[n]

###K.状压dp

题目大意为给定一棵有向树，每个节点有ci,pi两个属性，给每个节点定一个[0,m]的值qi。 节点i的权值为ci∗| j| |ci−qi| > |cj−qj|,j是i的后代节点 |。 树的权值为所有节点权值之和。问树的权值为S的方案个数。

每个点可取的状态有m种，显然不能直接状压，我们设f[k][sta][sum]表示当前节点中满足|ci−qi|<=k的点的集合为sta，且当前权值和为sum的状态数。

那么我们枚举sta的子集mask，mask中的点权值为k，其余点权值小于k，则状态转移方程为f[k][sta][sum] += dp[i-1][sta-mask][l]

其中l=sum-∑pj × |subtree[j]∪opt|,j属于mask，subtree[j]为j的后代的集合。

但是枚举子集的子集时间复杂度为3^n，难以承受。

我们发现题目也保证了当父亲节点的标号一定小于当前节点的标号，因此只要我们按照节点的标号从小往大枚举，就不会有重复计算的问题。转移方程为f[k][sta]sum] += f[k][sta-j][l]。

其中l=sum-pj∗|subtree[j]∪opt|

还需注意到我们可以压缩一维空间：

f[sta][sum] += f[sta-j][l];

代码稍后会附上。