前两天由于队友有事,所以在CodeForces的geym里面找了两套题来做,都是很水的题目,只有一两道数据结构比较恶心。今天我们又继续开始Regional的训练。今天题风比较奇怪,卡在了一道在有向图中找奇环的题目上。导致有几道题没读。
A. Coin Swap
知识点
性质 + 二分图最优匹配
题目大意
给一个$n$个点$m$条边的无向图,每个点上有一个棋子。点有黑白两种颜色,棋子也有黑白两种颜色。且黑色的点和黑色的棋子数目相同。每次操作可以交换一条边的两个顶点上的两个棋子。问最少交换几次才能使得所有棋子正好在相应颜色的点上。
做法
我们可以发现这样一条性质:如果果一条边的两个顶点上放的棋子颜色相同,那么这条边一定不会进行交换。所以,我们直接拿出所有的黑色棋子以及所有的黑色点,构成一个二分图。这个二分图中每个棋子都向每个点连一条边,长度就为在图上的这两点的最短路。之后我们需要跑一个权值最小的完全匹配。这可以通过km算法,将边权置为负的来跑最优匹配。这样跑出来的就一定是合法且最优的解。
B. Equilibrium State
没读题
Grid
知识点
二分图匹配 + 网络流
题目大意
给出一个$n \times m$的矩阵,矩阵中的每个格子中有一个$0$~$1000$的数字,每次操作可以选择相邻的两个格子,将这两个格子中的数字同时减$1$(如果原数字已经是$0$则不再减)。问至少需要几次操作才能将所有的数字都变为$0$。
做法
首先,需要的操作数上限为矩阵中所有数字之和。
由于是矩阵,因此原图可以视为一个二分图。相当于每有两个相邻格子中的数字同时大于$1$,那么我们可以仅通过一次操作就将这两个数同时减一,即减少了一次操作。这样匹配的次数越多,那么我们的操作次数就越少。
因此可以构造一个网络流模型。将矩阵进行黑白染色后,黑点视为一个集合,白点视为一个集合,从源点向每个黑点连一条流量为该点的数字的边,从每个白点向汇点也连一条流量为该点数字的边,每个黑点向和它相邻的白点连一条流量为$INF$的边。之后跑最大流即可求出可减少的次数最多为几次。用总的次数减去该最大流即为答案。
D. Kernel
没读题
E. Log Jumping
签到题
题目大意
给出$n$个数字,先要把这$n$个数字排成一圈,使相邻的两个数字的差的最大值最小,问该最小值是多少
做法
如果将原数排个序,我们将最大的数放在中间,之后将次大数放在一边,第三大的数放在另一边……这样交替的放,可以证明这样会使最大的差值最小
F. Odd Cycle
知识点
图论
题目大意
给出一个$n$个点$m$条边的有向图,在图中找出一个长度为奇数的环并输出方案。
做法
未解决
G. Path
知识点
计算几何
题目大意
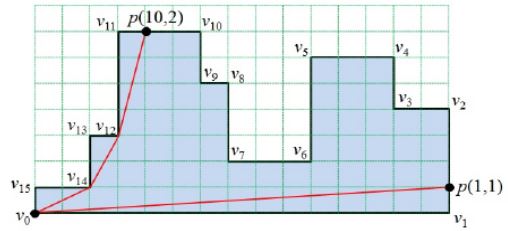
给出一个如下图所示的图形。我们只能在这个图形内部走。给出位于图形边界上的一些点。我们要求从图形左下角点到所有点的距离的和的最小值
做法
等待Ruclion更新
H. Polynomial
未解决
I. Stock
签到题
题目大意
有一种物品,在n天内,每天的价格不同,每一天你可以选择买一个这种物品,或卖出任意数量的这种物品或什么都不做。问你最后的收益最大为多少。
做法
只要某天之后有一天的物品价格大于当天,则在这一天选择买入,如果没有则选择卖出。这可以保证收益最大。
J. 3-Primes Problem
签到题
题目大意
给出一个数$k$($7 \leq k < 1000$),找出三个质数使其相加等于k
做法
由于数据范围很小,我们直接枚举两个质数,在判断第三个数是不是质数即可
K. Tree Edit
知识点
树形dp
题目大意
做法
等待Ruclion更新
L. Wheel of Numbers
签到题,安题意做就行。